Practice: Math Tools
Practice in Action
Math Tools include pictures, rulers, symbols, technology, and concrete materials such as beans, blocks, or other manipulatives that allow students to problem solve. Math tools can help students measure, count, sort, and evaluate math problems.
Find out from school-day teachers the concepts and skills your students are learning and how math tools can enhance their learning. Develop activities in which students can play with different objects and learn to use tools to problem solve. Provide an assortment of tools to tap students' interest and help them see a variety of approaches to problem solving. Make connections between the tools and the corresponding mathematical idea you want students to learn.
It is tempting to get out the manipulatives and show students how to use them, but math tools work best when students can figure out how the tools can help them solve a problem. Finally, allow students to discuss how specific tools contributed to their thinking about mathematics.
When tools are used productively to teach and learn mathematics, students see connections among objects, symbols, language, and ideas. Students who are provided with mathematical tools use them to explore concepts and to build mathematical understanding.
Additionally, tools help students think flexibly about mathematics, use creativity to solve new mathematics problems, and explore mathematics with less anxiety. Because the nature of afterschool is active and social, afterschool settings are ideal for allowing students to explore, test, build, think, talk, connect, and reason with mathematical tools.
Math tools such as beans, graphs, rulers and computers are important aids to help all students problem solve. Students can use tools to both represent and evaluate problems. This is especially true for ELLs. Instructors of ELLs can also use tools to represent a problem when a language barrier exists. In the same way, an ELL can use tools to demonstrate his or her understanding of a problem and a possible solution.
Some ELLs may not have previously used tools such as an American ruler or an Excel spreadsheet. However, for these students, gaining experience with a new tool is more valuable than getting the right answer to an activity question.
Tools often require special language and instructions. For instance, a standard American ruler requires knowledge of fractions, inches, and feet. Similarly, a spreadsheet uses columns and rows. To use tools effectively for problem solving, ELLs may need to know the vocabulary, language, and number forms associated with their use. Check the ELL Teaching Tips and Language Goals links for sample lesson activities to preview the vocabulary, problem-solving instructions, and language patterns that will help ELLs communicate and collaborate with classmates and make the best use of their learning tools.
Planning Your Lesson
Great afterschool lessons start with having a clear intention about who your students are, what they are learning or need to work on, and crafting activities that engage students while supporting their academic growth. Great afterschool lessons also require planning and preparation, as there is a lot of work involved in successfully managing kids, materials, and time.
Below are suggested questions to consider while preparing your afterschool lessons. The questions are grouped into topics that correspond to the Lesson Planning Template. You can print out the template and use it as a worksheet to plan and refine your afterschool lessons, to share lesson ideas with colleagues, or to help in professional development sessions with staff.
Lesson Planning Template (PDF)
Lesson Planning Template (Word document)
Grade Level
What grade level(s) is this lesson geared to?
Duration
How long will it take to complete the lesson? One hour? One and a half hours? Will
it be divided into two or more parts, over a week, or over several weeks?
Learning Goals
What do you want students to learn or be able to do after completing this activity? What skills do you want students to develop or hone? What tasks do they need to accomplish?
Materials Needed
List all of the materials needed that will be needed to complete the activity.
Include materials that each student will need, as well as materials that students
may need to share (such as books or a computer). Also include any materials that students or instructors will need for record keeping or evaluation. Will you need to store materials for future sessions? If so, how will you do this?
Preparation
What do you need to do to prepare for this activity? Will you need to gather
materials? Will the materials need to be sorted for students or will you assign students to be "materials managers"? Are there any books or instructions that you need to read in order to prepare? Do you need a refresher in a content area? Are there questions you need to develop to help students explore or discuss the activity? Are there props that you need to have assembled in advance of the activity? Do you need to enlist another adult to help run the activity?
Think about how you might divide up groups―who works well together? Which students could assist other peers? What roles will you assign to different members of the group so that each student participates?
Now, think about the Practice that you are basing your lesson on. Reread the Practice. Are there ways in which you need to amend your lesson plan to better address the key goal(s) of the Practice? If this is your first time doing the activity, consider doing a "run through" with friends or colleagues to see what works and what you may need to change. Alternatively, you could ask a colleague to read over your lesson plan and give you feedback and suggestions for revisions.
What to Do
Think about the progression of the activity from start to finish. One model that
might be useful—and which was originally developed for science
education—is the 5E's instructional model. Each phrase of the learning
sequence can be described using five words that begin with "E": engage, explore, explain, extend, and evaluate. For more information, see
the 5E's Instructional Model.
Outcomes to Look For
How will you know that students learned what you intended them to learn through this
activity? What will be your signs or benchmarks of learning? What questions might you ask to assess their understanding? What, if any, product will they produce?
Self-Evaluation
After you conduct the activity, take a few minutes to reflect on what took place.
How do you think the lesson went? Are there things that you wish you had done differently? What will you change next time? Would you do this activity again?
Sample Lessons
Students compare cell phone plans by analyzing tables, graphs, and equations, and make recommendations for the "best" phone plan, based on their analysis.
Cell Phone Plans (2-5)
Duration: 30 to 45 minutes
- Communicate about mathematics (e.g., use mathematical language and notation effectively, compare their own thinking with other students' thinking)
- Use strategies to understand new math content
- Develop efficient solution methods
- Construct algorithms effectively
- Understand equivalent representations of a problem situation or mathematical concept
- Solve problems involving rate as a measure
- Understand the concept of algebraic expressions and equations
- Understand properties of graphs and the relationship between a graph and its corresponding equation (e.g., y-intercepts and slope)
- Use a variety of models (e.g., written statement, algebraic formula, table of input-output values, graph) to represent functions, patterns, and relationships
- Use a variety of methods (e.g., graphs and algebraic methods) to solve systems of equations
- Use tools to understand mathematics in new ways
- Teacher's Guide (PDF)
- Student Worksheet (PDF)
- Pencils (colored, as needed)
- Paper (graphing and other, as needed)
- Ruler or straightedge
- Graphing calculators
- Print out the accompanying PDFs and familiarize yourself with the scenarios students will be involved with.
- If necessary, make time to share the lesson with a day time mathematics instructor to converse about the standards and mathematics involved, and practice working through the graphs on a graphing calculator and/or by hand.
- Organize students in small groups (to allow for discussion partners, if necessary).
- Make sure all materials and tools are available for all students.
- Prepare a brief introduction of the problem the students will be involved with and the tools they can use to solve it. The goals of this discussion are to clarify the task and pique students' interest in the problem.
- Briefly introduce the problem. Students should find choosing a cell phone plan interesting and relevant. You might ask how much students (or their parents) pay for their cell phones. You might also ask how students would decide which cell phone plan to purchase and if there are any tools that might help them make a decision.
- Provide students with the two different cell phone plans (see PDF). Before they do any analysis, ask them which they would choose, and why. Next, have students begin working on the analysis of the cell phone plans.
- Students might find it helpful to work together, and to bounce ideas off of you. Stay involved with students' work, and ask questions as you circulate among them. Watch for students who get stuck or don't know how to create a graph. Also, stay tuned in to how students are using mathematical tools and provide appropriate guidance as necessary. (Note: The calculator makes sophisticated mathematics accessible to students who might not be able to "jump in" algebraically. (A goal of this practice is for students to use the tools to see and understand the mathematics in ways they otherwise might not.)
- Depending on student's autonomy and problem-solving experience, they may be able to create a graph on their own, or they may need additional guidance from you. Base your decision to scaffold the graphing activity on your knowledge of students' background. Use the Teacher's Guide (see PDF) for specific information. The more students can accomplish and figure out on their own, the better.
- The x-axis should be labeled with the number of minutes, and the y-axis with cost (the cost depends on the number of minutes; the cost is the dependent variable, and thus belongs on the y-axis). You might want to discuss this with students.
- Some students may not be familiar with the graphing calculator. In this case, you may choose to share some of the examples from the Teacher's Guide with students to help them get started. Typically, setting an appropriate window is problematic for students. The more they can see the connection between the graph they draw on graph paper and what they see on the calculator, the better
- An extension activity is included for students who are experienced with algebra and need a challenge. Or, you might extend the activity to two days and ask all students to complete the extension problem. The extension adds a third phone plan for students to analyze.
- All students are engaged and actively seeking answers
- Students communicate effectively about mathematics (e.g., use mathematical language, compare their own thinking with other students' thinking, gain clarification from each other
- Students use strategies effectively
- Students develop efficient solution methods
- Students construct algorithms effectively
- Students use a variety of models (e.g., written statement, algebraic formula, table of input-output values, graph) to represent functions, patterns, and relationships effectively
- Students use a variety of methods and tools (e.g., graphs and algebraic methods, graphing calculators and tables) to solve systems of equations effectively
- Students use tools (e.g., graphs, calculators) to see connections among algebraic ideas and symbols
- Students access sophisticated mathematics through their use of tools
Students use a variety of measurement skills, tools, and strategies to find the area of their handprints and foot prints.
Hands and Feet (2-5)
Duration: 30 to 45 minutes
- Understand length, width, height, and area, and how they connect
- Use specific strategies to estimate measurements
- Select and use appropriate standard (inches, for instance) and nonstandard (arbitrary lengths of string, for instance) units and tools of measurement
- Test predictions and communicate mathematical reasoning
- Graph paper and unlined paper
- Pencils or colored pencils
- Ruler and protractors
- Geoboards (optional)
- Directions for each center
- Use the materials provided to trace your hand and foot separately.
- Make a prediction of whether your hand or your foot takes up more space.
- Find out if your prediction is correct.
- Prepare directions and materials.
- Print Measurement and Geometry: Hands and Feet (PDF)
Some students will understand length, width, and area more quickly than others and may not need guidance on the use of a ruler or protractor.
Be sure that students maintain the proper units of measurement as they proceed (centimeters, inches) and that all measurements for one object are taken using the same units. Students who are measuring will also need to use the formula for calculating area, or the space an object takes up (area = length x width).
Allow them to come up with the formula on their own or have a conversation about what they might do with their measurements before you provide it for them.
Students who are just learning these concepts may use nonstandard units of measurement, like counting the squares on the graph paper or simply guessing by comparing the size of their hands and feet.
These students will need to estimate some squares in portions (halves, quarters) and will also need to keep track in some way of what has been counted. Coloring or marking counted spaces in some way will be helpful. However students decide to tackle the problem, allow them to explore on their own before stepping in to offer a suggestion.
- Pose the question that students will answer during this activity, Which do you think takes up the most room, your footprint or your handprint?
- Allow students time to brainstorm and make predictions without tracing their hand/ foot.
- Use the PDF to review length, width, and area with students.
- Ask students to trace one hand and one foot on graph paper, then predict which is bigger. Students may count the squares on the graph paper as a strategy for making predictions.
- Next, ask students to measure the length and width of their handprints and footprints.
- When students have measured length and width, ask them to calculate the area of each one to test their predictions.
- Circulate and pose questions as students are working. Encourage students to work together to problem solve.
- Finally, ask students to report in on which was bigger, how they came to their answers, if their predictions were correct, and what they learned.
- Student participation and engagement
- Students work together and use tools to problem solve
- An understanding of nonstandard units of measurement (guessing size, counting graph paper squares) as well as standard units of measurement (measuring inches and centimeters, calculating the area)
- Answers that reflect an understanding of length, width, and area
- The ability to make and test predictions
- Since the goal of this activity is for students to strategize a method to verify their prediction of which is bigger, their hands or their feet, it is not necessary for ELLs to use inches to do so. Unless they were born in the U.S., they are probably more familiar with the metric system.
- Have ELLs partner with English-speaking students so that ELLs can offer assistance with centimeters and the English speakers can offer assistance with inches if needed.
- Reword the question, Which do you think takes up the most space, your footprint or your hand print? to Which drawing takes up the most space, your footprint or your handprint? Use gestures and point to help ELLs understand the question being posed.
- Point out or elicit from students that the sample measurements on the handout are in inches. Ask students for other ways to measure; ask ELLs to share how the word "centimeter" and its abbreviation can be written.
- Watch and observe as students work with partners to determine which takes up more space. ELLs may already have this understanding. They may be able to demonstrate the concept of area better than they can explain it.
- Make sure all students write and use measurement units when describing the length, widths, and areas of their hands and feet. Even though an ELL might have used centimeters, hearing another student show his or her hand and give its measurement in inches allows the ELL to make comparisons between centimeters and inches.
- Write up and model the sentence structures below. The after-school instructor should point to the words of the sample sentences so ELLs can follow and share their own sentences using the models.
My foot (or hand) is ________ inches/centimeters long.
My foot (or hand) is ________ inches/centimeters wide.
My footprint (or handprint) is ________ inches/centimeters.
Students watch the growth of rock candy over a given length of time, describe the varying rate of change they observe, and graph these changes.
Growing Rock Candy (3-5)
Duration: 1 week of observation followed by a 1-hour lesson
- Recognize patterns and the rules that explain them
- Use mathematics vocabulary to discuss observed growth patterns
- Select and use appropriate tools to make measurements
- Organize and display data in simple charts and graphs
- Observe growth patterns from a table and graph
- Graph paper
- Pencils (2 per student)
- Ruler (cm)
- 6-inch piece of string (per student)
- 3 cups of granulated sugar (per student
- Cup of water (per student
- Clean glass jar (per student)
- Food coloring
- Stove
- Saucepan
- Spoon
- Prior to the activity, make the rock candy solution. Or, you might choose to incorporate cooking into the activity.
- In a medium saucepan, heat two cups of the sugar and the water. Stir until the sugar is completely dissolved. Gradually add a few drops of the food coloring and the additional sugar, stirring continuously until all the sugar is dissolved.
- Designate an area where the rock candy can grow without being disturbed for approximately one week. Students will need access to this area in order to measure growth. Limit movement of the rock candy once it has started growing.
Sample Table for Rock Candy Growth
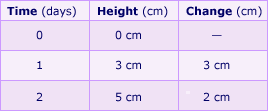
Change is calculated by subtracting previous day's height from current day's height.
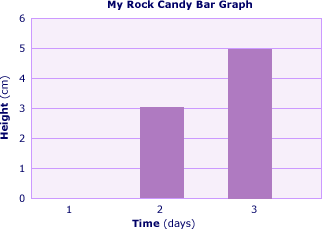
Using graph paper, allow students to use either bar or line graphs to represent the growth pattern of their rock candy. A bar graph illustrating the information above might look like this:
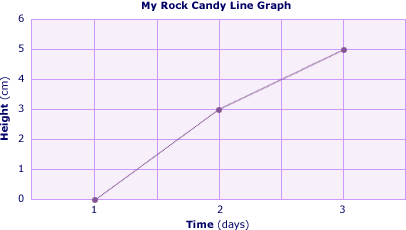
A line graph illustrating the growth of the rock candy might look like this:
A printable PDF version of this page is also available. (PDF)
- Using the rock candy solution, set up the growing area for the candy. Pour the solution into a clean glass jar, tie the string to the pencil, and suspend it across the mouth of the jar so that the ends hang into the sugar water. See Algebra: Growing Rock Candy (PDF).
- Have students develop a table containing three columns: time (days), height (cm)[[comma]] and change (cm). They should put 0 in the top row under "time" and "height," leaving the space blank under "change."
- On day two, give students 10 to 15 minutes to measure their rock candy growth. The students should remove the string from the water and carefully measure the height of the rock candy. Add this information to the next row of the chart, this time filling in the space under "change" (today's height minus yesterday's height).
- Have students continue charting growth over multiple days until measurable growth has ceased.
- On the final day, have students use graph paper to give a visual representation to the candy growth. One axis should be height and the second axis should be time.
- Using this data, have students describe how the rate of growth varied over time. Encourage them to look not only at the height per day, but at what has happened between the recorded heights.
- Use of vocabulary (such as slow, fast, increase, decrease) to describe what has happened between each measurement taken
- An ability to focus not simply on the height measurement but what has happened between the recorded heights
- Comments and answers that indicate that students are listening to, monitoring, and applying the problem-solving strategies of their peers
- Partner ELLs with strong English-speaking students, so that English speakers can demonstrate and model instructions.
- On the board or chart paper, write up the important steps for students to follow to make candy and measure and record growth. Model, demonstrate, and have ELLs take turns reading various steps so that directions are clear. Leave the steps posted on the board or wall so that instructor and ELLs can refer to them as needed during the project.
- Provide opportunities for ELLs to share their data using numbers and the appropriate measurement units.
- Since English speakers might use ordinal numbers such as "first day" and "second day" to refer to Day 1 and Day 2, highlight and practice these number forms (first, second, third, etc.) with ELLs. Also, consider displaying and reviewing the days of the week in order to clarify how many days have passed between measurement dates.
- Highlight the present and past forms of the verb "to be" so that ELLs can describe how their candy has changed. Write the following sentences on the board so ELLs can share their data. On the first day (on Day 1) my candy was ______ centimeters high. Now (today) my candy is _______ centimeters high.
Students predict how many M&Ms are in a bag, collect data, and graph their findings in MS-Excel.
Graphing Candy with Excel (5-8)
Duration: 45 to 60 minutes
- Collect data through observations
- Represent data using tables and graphs (by means of MS-Excel)
- Use data for a variety of purposes (formulating hypotheses, making predictions, testing conjectures)
- Determine probability using simulations or experiments
- Enter data into a spreadsheet, use formulas to update solutions automatically, and create a pie graph
- Use ratios and proportions to represent relationships among quantities
- Explain and justify their thinking
- PC or Macintosh with an electronic spreadsheet application such as MS-Excel, word processing software such as MS-Word for writing summaries of findings, access to the Internet (optional)
- Small bags of M&M's (1 per student)
- Students need to have basic keyboarding skills; know how to open, close, and save documents; and open and navigate a software application such as MS-Excel and MS-Word.
- Teachers need to know how to open, close, and save documents; how to create an MS-Excel worksheet (including using formulas); and use MS-Word.
A ratio is a comparison between two numbers, usually represented by two numbers separated by a colon. Students can find multiple ratios with the colored candies. For example, you may ask them to find the ratio of yellow candies to brown candies. If there are seven yellow candies and nine brown candies the ratio of yellow to brown candies would be represented by 7:9. When using ratios, the order of numbers and words are important. The numbers should be written in the same order as stated. For example, in the ratio of yellow to brown candies, the number of yellow candies is written in front of the colon while the number of brown candies is written after.
To compare ratios, change the ratio to a fraction, with the first number as the numerator and the second as the denominator. Using the example above, the ratio 7:9 would become 7/9. The ratios are equal if the fractions are equal, for example, 7:9 = 14:18 because 7/9 = 14/18.
- To begin this lesson, have students estimate the number and color of candies inside their small bags.
- After the estimations have been made, students open their bags to sort, classify, count, and record the M&M's. Students are then directed to write ratios to represent their findings. Technology plays an integral part in the rest of this lesson. After they collect data, students use an electronic spreadsheet to create a graph of their findings. Please review and print the detailed description in Data Analysis and Probability: Graphing Candy with Excel (PDF).
- When students finish collecting data, they will compile a set of everyone's findings to estimate the number and color of M&M's in a mystery bag.
- In order to win the mystery bag, students must not only make a conjecture but also explain their reasoning using the data sets.
- Student participation and engagement
- Answers that reflect an understanding of prediction
- An ability to explain math reasoning
- Ratios that represent the actual findings
- Reasonable conjectures based on the class set
- The appropriate use of a spreadsheet to create a graph
- Encourage English-speaking partners to model and share counting and recording duties with ELLs. Since the range of numbers is not very high, ELLs can be responsible for counting out in English and recording the numbers of each color candy and the resulting ratios.
- When introducing how to write and read ratios, the afterschool instructor should write some examples on the board with the word "to" written above or below the colon. An ELL could understand the ratio of 4:2 as "4 2 2" if the colon and the corresponding word "to" are not visually clarified. This could be a teachable moment, where you differentiate between the number 2, and the word "two" and its homophone "to"—in this case represented by the colon.
- Have beginning ELLs orally count out numbers of each color candy, stating the number and color for the total (for example, five brown, six yellow, etc.).
- Give ELLs opportunities to practice reading ratios of colored candies for their groups and for the entire class.
Students use counters, such as pinto beans, and a variety of problem-solving techniques to estimate and determine the solution to Raul's Apples.
Raul's Apples: Word Problem (6-8)
Duration: 30 to 45 minutes
- Use problem-solving strategies and manipulatives to solve a problem involving number sense
- Find a solution to a real-world problem using manipulatives
- Develop and use strategies to judge the reasonableness of results
- Work together to problem solve
- Number and Operations: Raul's Apples: Word Problem (PDF)
- Beans (about 100 per small group)
- Make sure that each group has enough beans to allow them to explore different scenarios.
- Think about the students in your group and determine whether they need calculators for the problem-solving task. The use of calculators should be determined based on the goals for the students.
- To use manipulatives to explore Raul's Apples, work the problem in reverse, using the beans to represent the apples Raul has.
- Encourage students to begin at the end of the problem, where it states that "he discovers that there are only two left," using two beans to symbolize this.
- When Raul encounters a friend he gives her "half of the remaining apples, plus two more." When working in reverse it is important to do every step in reverse. Therefore add two more beans to the two already on the table, this represents the reverse of "plus two more."
- Then, to find the reverse of "half the remaining apples," double the apples on the table, so that there are now eight (8) beans. Continue this process with each step of Raul's trip to find the number of apples in the bag at the beginning of the problem.
- Organize students into small groups of three or four.
- Hand out the Raul's Apples: Word Problem (PDF) and allow students time to read and begin work on the problem.
- Ask students to begin sharing their thinking in their small groups.
- Provide them with beans to help them figure out the problem. Ask how the beans might help. Listen for a variety of ways in which students think about the beans. Help students see how the beans can be used to represent the apples in the problem.
- As students find answers to the problem, ask them to justify their thinking to you. How did you use the beans? Were they helpful? Why did you choose to start with that number of beans? Have them prepare a presentation for the entire group where they share their thinking about the problem.
- Encourage students who have solved the problem in different ways to share their thinking so that a variety of solution strategies are shown.
- Students think about using the beans to solve the problem in a variety of ways (guess and check, working backwards, etc.)
- Students justify their use of manipulatives to find a solution to the problem
- Comments and answers that indicate that students are listening to, monitoring, and applying the problem-solving strategies of their peers
- ELLs may have difficulty comprehending word problems and extracting the important mathematical information. Using beans to represent apples is a great way for nonverbal ELLs to demonstrate their understanding. However, substituting one object for another may confuse some beginning ELLs in their basic understanding of the problem.
- If possible, read through the problem with beginning ELLs twice: once for general meaning and once to highlight mathematical operations. It may help to group ELLs together when you do this.
- As you read, ask questions to check comprehension, such as, Does Raul have more apples or fewer/less? Did he add or subtract?
- On the second reading, ask students to underline the key phrases which indicate a mathematical operation, such as "give half of his apples to the needy" and "plus two more."
- Have students write the mathematical expression above each of the underlined phrases. Once they have highlighted the relevant phrases, noted the respective mathematical operations, and estimated the result, they are ready to begin tackling the larger problem using the beans or other methods.
- It may be helpful to create a word bank to practice key phrases that indicate the various operations. Many of these words are similar in Spanish and other Latin-based languages.
+ - x / addition subtraction multiplication division plus minus times half add subtract multiply divide total remainder product quotient more fewer (less) - Give ELLs an opportunity to read aloud their final number sentences and solutions and the inverse of that equation in order to check their solutions.
- Since participation and communication are the most important goals for beginning ELLs, it may not be critical for them to correctly use the words "fewer" and "less" to describe quantities that are either countable or uncountable (such as in fewer apples, less sugar). Raul's Apples uses apples, so "fewer" is the correct adjective. Generally, if you can count something like apples or fish, it's countable and takes "fewer" as a comparative adjective. On the other hand, things that you cannot count, like milk and sand, are uncountable and take "less" as their adjective. Check with the ESL teacher to determine if this concept has already been introduced. If so, this lesson provides a good context in which students can practice. Of course, instructors should always model correct language usage.
Students use nonstandard units of measurement to find the area of their handprint or footprint, compare findings, and discuss their discoveries as a group.
Crafts: Cereal Hands and Feet (K-3)
Duration: 20 to 30 minutes
- Use nonstandard units of measurement
- Understand the basic concept of area
- Compare and order objects using given attributes
- Explain and justify their thinking
- Construction Paper
- Pencils or Markers
- Glue, tape
- Box of similarly shaped/sized cereal (Cheerios, Fruit Loops, Chex
- Sort through the cereal box and discard any pieces that are broken or not of equal size.
- Young children or students with special needs may not have the dexterity to accurately trace their hand or foot. In this case, plan on helping this student. Asking another student to help may also be appropriate.
- Ask children to trace around their hand or foot on construction paper to make a print.
- Have students glue cereal pieces on to their print so that the pieces are close together but not overlapping.
- Have students count the number of pieces it took to completely cover their print and record this number below the print.
- Encourage students to share the number of pieces it took them with the group.
- The number of pieces will vary; ask students why there are so many different answers. (Responses might include different-sized hands or cereal, or that some pieces are closer together than others). Discuss with students the importance of using a standard unit of measurement—for instance, that it gives a consistent basis for comparison.
- If some students spread their fingers before tracing their hands, and others did not, ask them if the number of cereal pieces to cover the hands would vary.
- Once the glue dries, have students order the prints from fewest to greatest number of cereal pieces. Have the students share their observations (e.g., "the number of cereal pieces gets larger as the print gets larger").
- Oral articulation of mathematical thinking, (e.g. use of appropriate mathematical vocabulary, rational to steps taken to solve problems)
- The ability to draw reasonable conclusions regarding area and nonstandard units of measurement
- Comments and answers that indicate that students are listening to, monitoring, and applying the problem solving strategies of their peers
Resources
www.nctm.org
National Library of Virtual Manipulatives for Interactive Mathematics
http://nlvm.usu.edu/
Virtual Manipulatives
http://otec.uoregon.edu/virtual_manipulatives.htm
Ball, D. (1992). Magical hopes: Manipulatives and the reform of math education. American Educator, 16 (1), 14-18, 46-47.
Carpenter, T.P., Fennema, E., Frank, M.L., Levi, L., & Empson, S.B. (1999). Children's Mathematics: Cognitively Guided Instruction. Portsmouth, NH: Heinemann, Reston, VA: NCTM.
Clements, D. H., & McMillen, S. (2002). Rethinking "concrete" manipulatives. In D. L. Chambers (Ed.), Putting research into practice in the elementary grades (pp. 252-263). Reston, VA: National Council of Teachers of Mathematics.
English, L., & Halford, G. (1995). Mathematics education: models and processes. Hillsdale, NJ: Lawrence Erlbaum.
Fuson, K. C. (1992). Research on whole number addition and subtraction. In D.A. Grouws (Ed.), Handbook of research on teaching and learning (pp. 243-275). Old Tappan, NJ: Macmillan.
Hiebert, J., Carpenter, T. P., Fennema, E., Fuson, K., Wearne, D., Murray, H., Olivier, A., & Human, P. (1997). Making sense: teaching and learning mathematics with understanding. Portsmouth, NH. Heinemann.
National Research Council. (2001). Adding it up: Helping children learn mathematics. J. Kilpatrick, J. Swafford, and B. Findell (Eds.). Mathematics Learning Study Committee, Center for Education, Division of Behavioral and Social Sciences and Education. Washington, DC: National Academy Press.
Sowell, E. (1989). Effects of manipulative materials in mathematics instruction. Journal for Research in Mathematics Education, 20, 498-505.
Stigler, J. W., & Barnes, R. (1988). Culture and mathematics learning. In E. Z. Rothkropf (Ed.) Reveiw of research in education, 15 p. 253-306. Washington, D.C.: American Educational Research Association.
Van de Walle, J. A. (2004). Elementary and middle school mathematics: Teaching developmentally. Boston, MA: Pearson Education, Inc.