SEDL INSIGHTS, Vol. 1, No. 4 (Winter 2014)
Teaching Mathematics Conceptually

Download PDF

It is entirely possible for students to memorize mathematics facts and manipulate numbers without having any deep knowledge of the concepts or processes involved. Memorization of rules and mastery of computation are not the same as true knowledge of mathematical concepts and ideas. The result of these practices is lower achievement in mathematics. According to the National Assessment of Educational Progress, only 42% of fourth-grade students and only 35% of eighth-grade students were at or above the proficient level in mathematics for their grades.¹ Similarly, only 44% of 2013 U.S. high school graduates are ready for college-level math.² If we want to help students develop the math skills that will enable them to enter STEM (science, technology, engineering, and mathematics) fields and allow the U.S. to remain competitive globally, we need to change some of our instructional strategies.

The insights described below are based on both my professional and personal experiences in the world of mathematics education—as a student simultaneously learning mathematics and English as a second language, as a secondary math teacher, as a professional development consultant at SEDL, and as a doctoral student surveying the existing research and curricula for mathematics instruction in the United States. Because of these experiences, I am calling on educators to shift their instructional focus. Instead of emphasizing misleading instructional language, short cuts, and the memorization of algorithms in math class, we can help students develop a deep understanding of mathematical concepts and identify connections between these concepts.³ Math teachers and instructional coaches should find these insights helpful in developing a deeper understanding of mathematics concepts, which should improve both instruction and student learning.⁴

Use instructional language with care.

Over time, common terms have become embedded in mathematics instruction; these terms often have a different definition in standard English than in mathematics. This can be extremely confusing or misleading—and inaccurate.

For example, a teacher might write the fraction 9/12 and tell students to reduce the fraction. The students are expected to follow the computation process and arrive at the solution 3/4. The careless use of the term reduce in mathematics is in direct contradiction to the standard English definition, “to make smaller.” Is it any wonder that some students get confused and think that 3/4 is smaller than 9/12? After all, 3 and 4 are smaller than 9 and 12. When I was a student, my teacher had a difficult time convincing me that those two fractions were equal. This was like many other experiences where I blindly accepted what the teacher said and plodded onward without any real understanding. Fortunately, new curricula and texts describe the process of changing 9/12 to 3/4 as simplifying rather than reducing.

Mathematics is a precise discipline, and teachers sometimes don’t realize that a slight deviation in language can render the content erroneous. Take for example the definition of an exponent. Some teachers drift from the correct version—the exponent indicates how many times the base appears as a factor—and instead inform students that the exponent tells you how many times the base is multiplied. Correctly expanded, the expression 7³ would be 7 • 7 • 7. Note that there are two multiplications, not three. Based on the careless definition, 7³ would be expressed as 7 • 7 • 7 • 7, which is, of course, incorrect. The slight deviation is well intended, but the result is a mathematically incorrect definition that is inadvertently taught to students and that affects future learning.

These shortcomings are not limited to language and can be due to omission rather than carelessness. The sign “–” is an excellent example. The tendency is to focus on interpretations such as minus, subtract, or negative. A poll of my colleagues, many of whom hold doctorates in education, revealed that most had never been taught that in certain contexts, this sign should be interpreted as meaning “the opposite of.” This interpretation is the least used but arguably the most important. Consider the expression –y. A common mistake is to pronounce this expression as “negative y.” This problematic pronunciation leads students to the false conclusion that the expression represents a negative number. What if y = –4? In this case, the value of –y is –(–4), or a positive 4. The difficulty in an expression such as –(–4) is that each negative sign must be translated differently. The negative sign outside the parentheses should be translated as “the opposite of,” while the sign inside the parentheses should be translated as “negative,” for the full interpretation, “the opposite of negative 4.” This interpretation enables students to understand better why the end result is a positive 4. In addition, the interpretation “the opposite of” not only simplifies and deepens content understanding but helps instruction by eliminating inaccurate rules such as “two negatives make a positive,” a rule that is yet another example of how mathematics instruction is sometimes far more complex than is necessary.

The above examples illustrate just a few ways that careless language can cause confusion in mathematics instruction. If a student is struggling to understand a mathematical concept, consider whether language is playing a role in the difficulty. By focusing on the language of mathematics, teachers can improve both content and instruction, ensuring that students gain a deep understanding of mathematics.

Another tradition deeply ingrained in mathematics instruction is a focus on algorithms and shortcuts without first ensuring conceptual understanding. Algorithms and shortcuts are not inherently bad; the key to using them to help rather than hinder understanding lies in the sequence of events that occur in learning mathematics concepts. Mathematics instruction must first ensure that students’ conceptual understanding is deeply embedded. When students have truly mastered a concept, they should be able to show all the detailed steps in a process, explain why those steps occur, and connect the process to related concepts. Once students reach this level of understanding, a teacher can then expose them to more efficient ways to express or perform those same processes.

Relying only on algorithms and procedures and focusing on shortcuts results in teaching efficiency, not mathematics. Shortcuts become the means to get to the answer with the unfortunate result of bypassing conceptual understanding, a tradeoff that may make it more difficult for students to understand more complex topics as they advance in school.

The process of simplifying a fraction provides an excellent example of the shortcomings of shortcuts. Refer to the examples below:

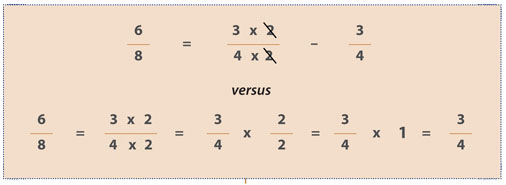
Although efficient, the first—and shorter—method leaves students with a fuzzy notion of what really happened. Contrast the shortened approach with the second, complete, process, which includes all the appropriate steps. By including each step, the complete process imparts a conceptual understanding of the multiplicative identity, the basic idea that any number multiplied by 1 remains the same. This fundamental property is the lynchpin for a deep understanding of what truly happens when you simplify a fraction. More important, the multiplicative identity is one of the primary algebraic tools used in solving equations.

If teachers simply show students the first method, students only learn that this “shortcut” is the way the teacher showed them and is what they are expected to do. Instead, by insisting that students use the full process and explain what they are doing, teachers help them establish a foundation for algebra. The detailed method that shows all the critical steps guides students through the process, resulting in a more thorough understanding of what simplifying a fraction involves and why it works.

Avoid naked numbers.

The phrase naked numbers refers to the prevalent use of numerals in isolation—without any descriptors, units, or context. Traditional instruction continually uses naked numbers, especially in the form of drill and practice geared to student memorization of facts or procedures. As a result, students can easily lose sight of the meaning of numbers and numerals, resulting in a diminished view of mathematics.

Without any context, teachers and students alike forget the meaning of the numerals and the key idea that they represent something. In looking at student performance on state-mandated exams, measurement is one of the areas where students historically perform poorly.⁵

Why is this? Based on my professional experience, naked numbers are one of the prime offenders lurking behind this poor performance. Measurement is not just about inches and pounds and liters. It must be perceived from a much broader lens. An 8 isn’t just that numerical symbol, and it isn’t necessarily 8 meters or 8 pounds. It can represent an infinite number of concepts from 8 elephants to 8 computers. Thus, we need to connect the idea of measurement to the larger idea of representation in mathematics. That is, students recognize that a numeral such as 8 is an incomplete expression and that it has meaning beyond a simple quantity. Students’ poor performance in the measurement strand could be a symptom of the system’s lack of emphasis on the language and representation of mathematics, and not just an indication that students have trouble with standard units of measure.

Unfortunately, the problems that have been discussed do not occur in isolation. These shortcomings often occur simultaneously and reinforce each other, compounding students’ confusion and misconceptions. Examine the problem 8 ÷ 1/2. Careless vocabulary is used when students are taught to interpret this expression as “how many times does 1/2 go into 8?” Add to this confusing language the lack of instructional emphasis on what those naked numbers represent. Just what do the 8 and the 1/2 actually mean? Even if students manage to block out the confusion, do they really understand the procedure? If students do attain the correct solution, do they have any idea what the correct answer,16, represents? Can they make sense of why the result of division was “larger” than the original number rather than “smaller”? The keys lie in understanding the question posed by the symbolism and knowing what the solution represents. Instead of using the infamous “goes into,” what if the students understood that the question was “How many halves are there in 8?” In turn, the students would understand that the quotient is 16 halves, not just the naked number 16. Now the “larger” answer makes sense because you have taken the 8 wholes and partitioned them into 16 smaller pieces, in this case, halves.

Help students make connections among concepts.

We have all heard the expression “work smarter, not harder.” It seems that teachers are continually expected to take on more and more responsibilities. In mathematics, one way to improve teaching and maximize instructional time is to find and utilize connections among mathematical concepts and ideas. As previously mentioned, making these connections takes advantage of the fact that knowledge about one topic comprises part of the knowledge of another. That common knowledge does not have to be taught again, but the teacher does have to recognize and make the connection. Recognizing the connections depends on deep understanding of math concepts and processes.

An example of an opportunity to make connections is the conceptual definition of an average. The key to that definition is a deep understanding of the related concept of multiplication. Many teachers define multiplication as repeated addition, but with that limited understanding, the progress to an understanding of an average comes to a screeching halt. It is true that multiplication is repeated addition, but the critical missing component is the idea that multiplication is repeated addition of equal-sized groups. The expression 3 × 4 can be expanded to 4 + 4 + 4, which represents 3 equal-sized groups of 4 each.

The next step to a deeper understanding of an average is to make a connection to the concept of division. Closer inspection of both multiplication and division at the elementary and middle school levels reveals that both processes involve the same basic three components: a total, a certain number of groups, and a constant size for each group. Multiplication and division are actually more similar than different. The only difference between the two processes is which of the components are known and which are unknown.

By focusing on equal-sized groups, students see that division is about equal sharing. With division, we start with a known total, whereas in an averaging context, the total is unknown. So, the key difference is the starting point. For an average, we must combine the different-sized groups into one total. After doing that, we are at the starting point of a division context. By making this connection, students realize that if division is about equal distribution, then an average is simply an equal redistribution. Let that soak in. Defining an average as an equal redistribution is simple, yet deep and conceptual, as well as applicable to a multitude of contexts; however, such a conceptual definition could not be attained without a connection to division and in turn, a connection to multiplication that is founded on a complete in-depth understanding of multiplication as a concept (and not just how to multiply).

The multiplication of decimals is another example of how making connections to related concepts can help students develop a deeper understanding of a process. Most of us are familiar with the old adage that laments not seeing the forest because of the trees. In this situation, it is easy to miss connections because they are almost too obvious. Consider the example below:

We are taught to pretend there are no decimals and complete the operation as if we are multiplying whole numbers. That is what is illustrated above. We are instructed to then count the number of places to the right of the decimal point in the two factors and that total is the number of places we should have to the right of the decimal point in the product. Thus, the solution above is .455. But, again, the question is why? The answer lies in making the connection to what this problem looks like when the decimals are expressed as fractions! Note the same problem below expressed in fractional form:

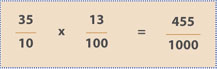
If we follow this process, we will see the forest! Note that we multiply the numerators, which are whole numbers. When we were multiplying the numbers in decimal form, most of us pretended that we were dealing with whole numbers—because that is what we had been taught. Now note that the result in the denominator is 1000. What is a simple way to divide by 1000? Move the original decimal point 3 spaces to the left. We realize that there was no magic, and the process with decimals makes sense via the fraction connection. Note the depth of understanding possible when we make this connection instead of following the rule without thinking about why it gives us the answer.

Lastly, it is critical to understand that we sometimes teach more than one concept or process simultaneously, yet the teacher and, in turn, the students do not make the connection and miss an opportunity to save extensive work and effort. Examine the process below as an example:

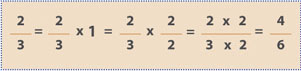
You will recognize this as the process involved in creating an equivalent fraction. Note that the critical idea is multiplication by 1 and also that there are no shortcuts. Now examine a similar example:

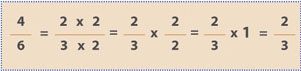
You should recognize that this is the process for simplifying a fraction (not reducing it) that was illustrated in Insight 1. If we examine both processes, we can easily make a connection. Note that one process is simply the other in reverse order. Using shortcuts can mask the similarities and hinder teachers from seeing the connection. By not taking shortcuts and insisting on illustrating the full process, teachers would actually do less work by teaching two ideas simultaneously.

Conclusion

Few would argue that there are opportunities to improve student achievement in mathematics in schools across the United States. We should learn from the anonymous adage that states: “If you keep doing what you’ve always done, you’ll keep getting what you’ve always gotten.” By focusing on instructional language, deep understanding of mathematical concepts, and the connection of related topics rather than algorithms and shortcuts, educators can help their students develop the math skills necessary for progress and innovation necessary in STEM fields.

How SEDL Can Help 

The insights described above are based on my book, The Problem with Math Is English: A Language-Focused Approach to Helping All Students Develop a Deeper Understanding of Mathematics. The book explores these insights in greater detail and provides a more in-depth explanation of how teachers can help their students develop a conceptual understanding of mathematics.

SEDL also offers a suite of free resources, professional development, and evaluation services for educators who are interested in improving mathematics instruction in their district or school. For more information, please explore the following resources:

• The Problem with Math Is English: A Language-Focused Approach to Helping All Students Develop a Deeper Understanding of Mathematics
• SEDL’s free resources for mathematics and sciences
• Common Core State Standards Video Series for Mathematics

Footnotes