|
The following syntheses which are based on the Curriculum and
Evaluation Standards for School Mathematics, outline some basic
aspects of teaching geometry. The accompanying activities, "Which
Container Holds the Most?" and "Building Houses,"
provide practical examples for translating the Standards recommendations
into classroom instruction.
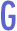 eometry
is an orderly way to describe and represent our inherently geometric
world. Basic to the understanding of geometry is the development
of spatial sense-an intuitive feel for our surroundings and the
objects in them. Spatial capabilities appear early in life, and
tapping into these strengths can foster an interest in mathematics.
Children who develop a strong sense of spatial relationships and
master the concepts of geometry are better prepared to learn number
and measurement ideas as well as other advanced mathematical topics.
Classroom experiences that focus on geometric relationships will
develop children's spatial sense. They should examine the direction,
orientation, and perspective of objects in space; the relative shapes
and sizes of figures and objects; and how a change in shape relates
to a change in size. Children can begin with activities that use
words like above, below, and behind and progress to using a computer
to reproduce a pattern-block design.
Evidence suggests that the development of geometric ideas progresses
through a hierarchy. Students first learn to recognize whole shapes
and then to analyze properties of a shape. Later they can see relationships
between shapes and make simple deductions. Instruction must consider
this hierarchy because, although learning can occur at several levels
at once, the learning of more complex ideas requires a firm foundation
of basic skills.
For middle school students the informal exploration of geometry
can be mathematically productive. Geometry at this level links the
informal explorations begun in grades KŠ4 to the more formal processes
of grades 9-12. Students draw inferences and make logical deductions
from geometric problem situations. They can also analyze their thought
processes and explanations. Allow sufficient time to discuss the
quality of their answers and to think about such questions as: Could
it be another way? Students should learn to use correct vocabulary,
including such common reasoning terms as and, or, all, some, always,
never, and if...then, as well as such descriptors as parallel, perpendicular,
and similar. Geometry has its own vocabulary including terms like
rhombus, trapezoid, and dodecahedron, and students need ample time
to develop confidence in their use of this new and unique language.
Definitions should evolve from experiences in constructing, visualizing,
drawing, measuring, contrasting, and classifying figures according
to their properties. Students who memorize a definition and a textbook
example or two are less likely to remember the term or its application.
Computer software allows students to construct two- and three-dimensional
shapes on a screen and then flip, turn, or slide them to view from
a new perspective. Explorations of flips, slides, turns, stretchers,
and shrinkers will illuminate the concepts of congruence and similarity.
Observing and learning to represent two- and three-dimensional figures
in various positions by drawing and constructing also helps students
develop spatial sense.
This synthesis is based on the chapters:"Geometry and Spatial
Sense" and "Geometry for Grades 5-8" from Curriculum and Evaluation
Standards for School Mathematics. Order from NCTM, 1900 Association
Drive, Reston, VA 22091. Telephone: 1-800-235-7566.
Geometry for Grades 9-12
Geometry in grades 9-12 encompasses algebraic and synthetic
(elementary euclidean) perspectives. The NCTM Standards recommend
that topics be integrated across all grade levels.The Standards
emphasize
- transformation and coordinate approaches,
- the development of short sequences of theorems,
- deductive arguments expressed orally and in sentence or paragraph
form,
- computer-based explorations of 2-D and 3-D figures,
- three-dimensional geometry,
- real-world applications and modeling.
In the study of geometry of two and three dimensions from an algebraic
point of view, students deduce properties of figures using transformations
and coordinates. They should be able to identify congruent and similar
figures using transformations, analyze properties of euclidean transformations,
and relate translations to vectors. Students headed for college
should also be able to deduce properties of figures using vectors
and apply transformations, coordinates, and vectors in problem solving.
The student who understands the interplay between geometry and
algebra has more power to construct and analyze problems. Objects
and relations in geometry correspond directly to objects and relations
in algebra. For example, a point in geometry corresponds to an ordered
pair (x,y) of numbers in algebra. A line corresponds to a set of
ordered pairs satisfying the equation ax + by = c. The intersection
of two lines corresponds to the set of ordered pairs that satisfies
the corresponding equations. Connections like these allow translation
between the two "languages" and permit concepts in one to clarify
and reinforce concepts in the other.
The synthetic component of 9-12 geometry allows students
to interpret and draw three-dimensional objects, represent problem
situations with geometric models, and apply properties of figures.
Students classify figures in terms of congruence and similarity
and apply these relationships. Geometry instruction should deepen
their understanding of shapes, their properties, and everyday applications.
Examples from such activities as recreation (billiards and sailing),
practical tasks (purchasing paint for a room), or the arts (perspective
in drawing) should be evident throughout the curriculum.
Give students the opportunity to work with three-dimensional figures
so they can develop spatial skills that are basic to everyday life.
Visualization also includes plane figures. Computer graphics software
that allows students to create and manipulate shapes makes conjecturing
and testing their attempts at two-dimensional visualization easier.
Computer microworlds such as Logo turtle graphics provide opportunities
for a great deal of student involvement.
Of course there are many opportunities for visualization that
do not use a computer. Exercises that require the student to draw
a diagram provide opportunities for reading mathematics and problem
translation.
This synthesis is based on the chapter "Geometry from a Synthetic
Perspective" and "Geometry from an Algebraic Perspective" from Curriculum
and Evaluation Standards for School Mathematics. Order from
NCTM, 1900 Association Drive, Reston, VA 22091. Telephone: 1-800-235-7566.
|
